Sharpe Ratio [Meaning, Formula, and Examples]

In the extremely dynamic business world of the 21st century, investments are a double-edged sword. On the one hand, a wise placement of capital promises large returns. On the other hand, it is always fraught with risks. When substantial sums are at stake, investors can't afford to act on a hunch. They need an objective yardstick to measure the potential prospects of their financial choices. And this is where the Sharpe ratio steps in.

The article provides the Sharpe ratio definition, explains how to find Sharpe ratio, and offers real-world examples of applying the Sharpe ratio formula.

What Is the Sharpe Ratio?

Introduced in 1966 by Nobel Prize laureate William F. Sharpe, the Sharpe ratio is used to evaluate an investment’s historical or expected performance relative to its volatility. It is calculated by subtracting a risk-free benchmark (typically a government Treasury rate) from the portfolio’s return and dividing that difference by the standard deviation of the portfolio’s returns.

To put it simply, the Sharpe ratio meaning boils down to its ability to tell an investor whether the potential or actual perks are (or were) worth the risk. Moreover, it helps determine whether the excess returns on investment are the result of smart, risk-adjusted decisions or if they are merely a matter of luck that may fade as market dynamics shift.

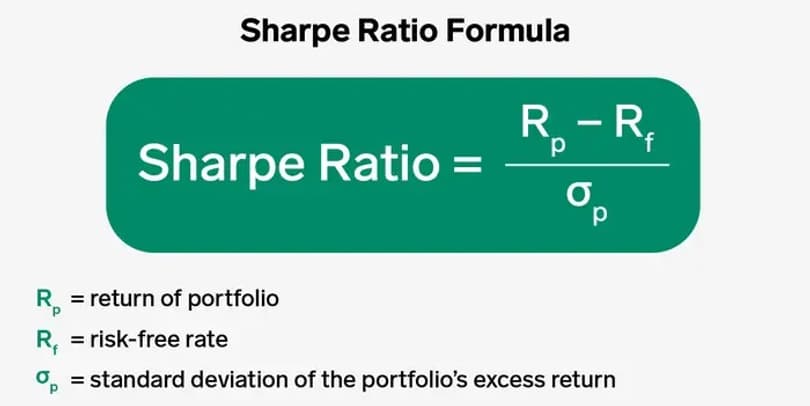
The formula to calculate the ratio is the following:

What do the variables in the equation denote?

• The return of a portfolio is the amount it has earned (or is forecasted to earn) during a specific period, expressed as a percentage of the initial investment.
• The risk-free rate is the benchmark figure that shows what you could have earned without any risks. Typically, Treasury securities serve as this benchmark.
• Standard deviation is a volatility index that reflects fluctuations in returns, both upward and downward over a given period. A higher number signals more risk.

Now, let’s illustrate the nitty-gritty of determining the Sharpe ratio.

How to Calculate Sharpe Ratio: A Step-by-Step Algorithm

Suppose you own a fund whose 5-year return (Rp) equals 30%. How good is its performance? To understand this, you should first find the 5-year Treasury rate (Rf). Let’s assume it is 4%. Meanwhile, the standard deviation (σp) during the same period is 20%. Thus, we have all variables on the table to calculate the Sharpe ratio.

Sharpe ratio = (30 – 4) ÷ 20 → 26 ÷ 20 → 1.3

Now we know the number, but what does it tell us? Sharpe ratios below 1.0 are generally considered poor or suboptimal, ratios between 1.0 and 1.99 are acceptable, ratios from 2.0 to 2.99 are very good, and ratios of 3.0 or higher are deemed excellent. With an eye on these criteria, the imaginary fund’s performance is found to be satisfactory.

The Sharpe ratio is a convenient and indicative metric to help you assess an organization’s risk-adjusted investment efficiency. However, you should use it cautiously since it has certain limitations.

First of all, the ratio doesn’t reveal whether any borrowed funds (also known as leverage) were used to generate returns. To learn this, investors should review the fund’s fact sheet (prospectus).

Secondly, the ratio doesn’t account for the duration of the return’s track record. For instance, a company with half a year of returns track record can annualize its performance, which makes a significant portion of the returns hypothetical rather than actual. It is the investor’s responsibility to clarify such details.

Finally, the ratio gauges total volatility. However, there is a key difference between an asset surging upwards and one that frequently plummeting to resume its initial index sometime later. Ironically, it is the upside volatility that investors seek, but its high absolute figures will lower the Sharpe ratio.

Allowing for these reservations, the Sharpe ratio remains a conventional tool for comparisons in real-world situations.

Real-World Scenarios of the Sharpe Ratio’s Application

Let’s juxtapose two companies: the Fidelity Contrafund (FCNTX) and the Vanguard Total Stock Market Index Fund (VTSAX). The former is an actively managed fund that aims to outperform the market. Over the past decade, the Fidelity Contrafund (FCNTX) delivered an average annual return of about 15.2%, with roughly 16–17% volatility, while the Vanguard Total Stock Market Index Fund (VTSAX) returned about 12.2% annually, with approximately 16% volatility. Which fund should you choose?

For consistency, one typically uses the 10-year US Treasury yield as the risk-free rate, which has averaged around 2.5% (annualized) over the past decade. Now, let the calculations begin.

Using these updated figures, FCNTX’s Sharpe ratio is roughly (15.2 – 2.5) / 17 ≈ 0.74, and VTSAX’s is about (12.2 – 2.5) / 16 ≈ 0.61. Both values are below 1.0 (generally considered suboptimal).

This indicates neither fund’s risk-adjusted return is particularly strong, and an investor should consider other factors beyond Sharpe ratios when choosing between them. It means that an investor should consider other aspects before pledging their money. For FCNTX, a tipping factor may be the potential for higher returns, whereas opting for VTSAX makes sense if you prioritize cost-efficiency and broad diversification.

The Sharpe ratio can also be used to assess not only the performance of companies but also that of investment managers.

For example, if Manager X yields 15% with 8% volatility and Manager Y yields 12% with 5% volatility (using the same assumed risk-free rate), Manager X’s Sharpe = (15–Rf)/8 and Manager Y’s Sharpe = (12–Rf)/5. With Rf around recent Treasury levels (~3–4%), Manager X’s Sharpe (~1.25) is actually lower than Manager Y’s (~1.40), suggesting Manager Y’s higher risk-adjusted performance.

Key Takeaways

The Sharpe ratio is a universally recognized metric for measuring the historical or potential investment performance of a company in relation to its possible risks. It is determined by subtracting the risk-free rate (typically based on government securities) from the returns of a certain portfolio and then dividing the result by standard deviation. Although not without its limitations, the Sharpe ratio remains a go-to benchmark for comparing the most promising risk-adjusted investment prospects.